SMART Exposure is BarnBridge’s second product. SMART Exposure allows users to automate position management between their ERC-20 assets. This product is for investors who want to passively maintain their asset pairs’ target allocations. There is a pool for each supported asset pair and in each pool there is a tranche for each target ratio. For instance, there are 2 pools currently, namely WETH/USDC and WETH/WBTC. Each pool has the tranches 50/50, 25/75 and 75/25. It can support up to 5 tranches.
A user’s position is rebalanced by keeper bots through Sushiswap’s flash swap if his position’s ratio deviates from the target ratio more than the threshold or if the time since the last rebalance exceeds the defined frequency.
When depositing ERC-20 assets into a tranche, a user receives exposure tokens (eTokens) in return. eTokens are also ERC-20 tokens, so they can be freely traded or even be utilized as collaterals by other protocols.
eToken’s name follows the format
bb_ET_TOKEN0RATIO0/TOKEN1RATIO1
bb = BarnBridge
ET = exposure token
TOKEN0/TOKEN1 = token symbols such as WETH, USDC and WBTC
RATIO0/RATIO1 = target ratios in percentage
Using SMART exposure can be cheaper than rebalancing your position by yourself because
You save on gas fees
The rebalance uses the price from Chainlink, so theoretically it should be cheaper
The 30,000 foot view
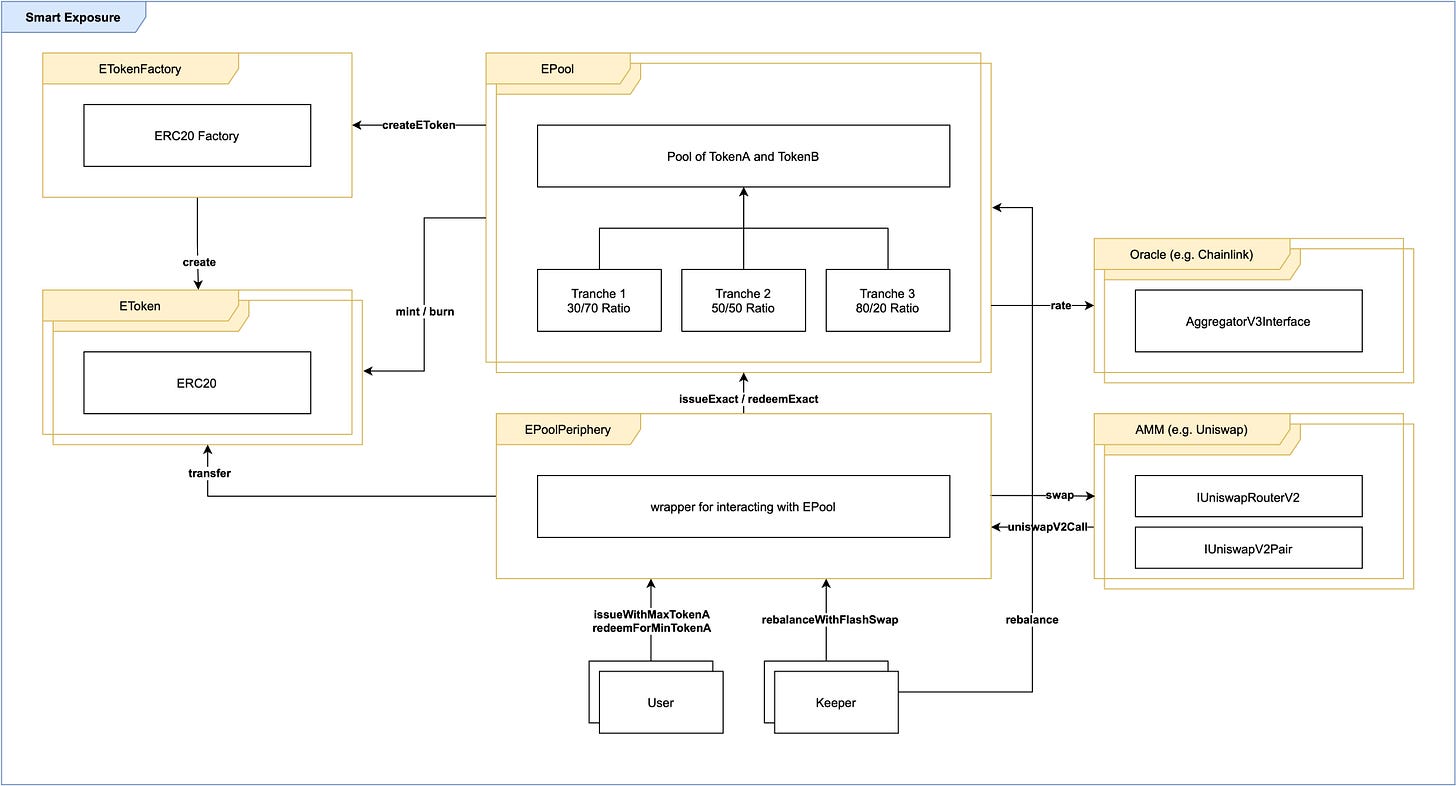
BarnBridge’s tech team wrote a very good specification with an architecture diagram. EPool is the core engine that holds different tranches of an asset pair. It mints and burns EToken created by the ETokenFactory, which represents exposure to a tranche. Users interact with the pool through EPoolPeriphery, although they can also interace with EPool directly. When a rebalance happens, the pool fetches the market price from Chainlink (AggregatorV3Interface) and then swaps using Sushiswap (IUniswapRouterV2).
EPool
EPool as the core engine holds all the data it needs to function. It holds a number of tranches (max 5).
struct Tranche {
IEToken eToken; /* Exposure token interface */
uint256 sFactorE; /* eToken's scaling factor */
uint256 reserveA; /* eToken's token A reserve */
uint256 reserveB; /* eToken's token B reserve */
uint256 targetRatio; /* token A ÷ token B target ratio */
}Each ERC-20 token in the pool has its own decimals and they can be different (WETH 18, WBTC 8, USDC 6). This is why we need a scaling factor for both reserve tokens and also the eToken in order to calculate target ratio and price correctly.
uint256 public immutable override sFactorA;
uint256 public immutable override sFactorB;Rebalancing can only happen if the pool’s reserve ratio deviates from the target ratio by more than its threshold. It uses rebalanceMinRDiv as the threshold. rebalanceMinRDiv is in percentage scaled by 1e18.
uint256 public override rebalanceMinRDiv;Rebalancing can only happen at particular intervals of time. The pool holds the interval as well as its last rebalance timestamp.
uint256 public override rebalanceInterval;
uint256 public override lastRebalance;Moving forward, we will look at the ETH/USDC 75/25 tranche, assuming ETH to be token A and USDC to be token B.
Issuing eTokens
Issuing eTokens can be done via EPoolPeriphery or Epool directly. We will look at EPoolPeriphery#issueForMaxTokenA. This function allows a user to mint a certain amount of bb_ET_ETH75/USDC25 for a max amount of ETH (maxInputAmountA).
First, the function makes sure the eToken is approved as a tranche and transfers maxInputAmountA ETH to the periphery contract.
require(ePools[address(ePool)], "EPoolPeriphery: unapproved EPool");
(IERC20 tokenA, IERC20 tokenB) = (ePool.tokenA(), ePool.tokenB());
tokenA.safeTransferFrom(msg.sender, address(this), maxInputAmountA);Then it uses EPoolLibrary#tokenATokenBForEToken to calculate the amount of ETH and USDC required to mint the number of eTokens required by the user. Let’s say the user deposits 100 ETH. There are 2 scenarios to consider.
Case 1: When the pool is empty
uint256 totalA = amount * sFactorA / tranche.sFactorE;
uint256 amountA = totalA - (totalA * sFactorI / (sFactorI + ratio));
amountB = (((totalA * sFactorI / sFactorA) * rate) / (sFactorI + tranche.targetRatio)) * sFactorB / sFactorI;The 100 ETH deposited has to be split into 75% ETH (18 decimals) and 25% USDC (6 decimals) to meet the target ratio. Assuming the price of 1 ETH = 2,000 USDC, an ETH/USDC ratio of 3 to 1, and eToken’s decimals as 18, it has 75 ETH (150,000 USDC) and 50,000 USDC.
totalEth = 100e18 x 1e18 ÷ 1e18
= 100e18
amountEth = 100e18 - 100e18 x 1e18 ÷ (1e18 + 3e18)
= 100e18 - 100e18 ÷ 4e18
= 75e18
amountUsdc = 100e18 x 1e18 ÷ 1e18 x 2000e18 ÷ (1e18 + 3e18) x 1e6 ÷ 1e18
= 100e18 x 2000e18 ÷ 4e18 x 1e-12
= 50000e18 x 1e-12
= 50000e6Case 2: When the pool is not empty
uint256 eTokenTotalSupply = t.eToken.totalSupply();
if (eTokenTotalSupply == 0) return(0, 0);
uint256 share = amount * t.sFactorE / eTokenTotalSupply;
amountA = share * t.reserveA / t.sFactorE;
amountB = share * t.reserveB / t.sFactorE;The calculation is simpler when the pool is not empty. The ETH and USDC amount to deposit are the reserves in the pool times the share of eTokens in the pool.
Swapping ETH for USDC
Since the user only provided ETH, the function has to swap ETH for USDC at Sushiswap. The ETH swap amount is the difference between maxInputAmountA and amountA. Its value should be equal to amountB.
require(maxInputAmountA >= amountA, "EPoolPeriphery: insufficient max. input");
uint256 amountAToSwap = maxInputAmountA - amountA;
address[] memory path = new address[](2);
path[0] = address(tokenA);
path[1] = address(tokenB);
tokenA.approve(address(router), amountAToSwap);
uint256[] memory amountsOut = router.swapTokensForExactTokens(
amountB, amountAToSwap, path, address(this), deadline
);Token transfers and reserves update
After getting USDC, the pool updates its reserves, mints eTokens, and transfers the tokens from the periphery.
(t.reserveA, t.reserveB) = (t.reserveA + amountA, t.reserveB + amountB);
t.eToken.mint(msg.sender, amount);
tokenA.safeTransferFrom(msg.sender, address(this), amountA);
tokenB.safeTransferFrom(msg.sender, address(this), amountB);The function then transfers the eTokens to the user and refunds any ETH leftover.
IERC20(eToken).safeTransfer(msg.sender, amount);
tokenA.safeTransfer(msg.sender, maxInputAmountA - amountA - amountsOut[0]);Rebalancing a pool
In order to rebalance all tranches in a pool, EPoolPeriphery#rebalanceWithFlashSwap can be called to conduct a flash swap at Sushiswap. A flash swap allows the pool to withdraw Sushiswap’s reserves with no upfront cost as long as the pool can repay the withdrawn amount with the correponding pair tokens or the withdrawn amount along with a small fee. In this code sample, we will assume ETH to have dropped to 1,800 USD.
First, it has to calculate ETH and USDC’s delta as well as its rate of change.
(uint256 deltaA, uint256 deltaB, uint256 rChange, ) = EPoolLibrary.delta(
ePool.getTranches(), ePool.getRate(), ePool.sFactorA(), ePool.sFactorB()
);The delta function loops through every tranche in a pool to calculate their individual deltas and rate of change.
for (uint256 i = 0; i < ts.length; i++) {
totalReserveA += ts[i].reserveA;
(uint256 _deltaA, uint256 _deltaB, uint256 _rChange) = trancheDelta(
ts[i], rate, sFactorA, sFactorB
);
(totalDeltaA, totalDeltaB) = (_rChange == 0)
? (totalDeltaA - int256(_deltaA), totalDeltaB + int256(_deltaB))
: (totalDeltaA + int256(_deltaA), totalDeltaB - int256(_deltaB));
}To calculate a tranche’s delta (using EPoolLibrary#trancheDelta), it has to first calculate the tranche’s current ratio. The formula is
((t.reserveA * rate / sFactorA) * sFactorI) / (t.reserveB * sFactorI / sFactorB)It has 75 ETH and 50,000 USDC in the tranche, so the current ratio is
((75e18 x 1800e18 ÷ 1e18) x 1e18) ÷ (50000e6 x 1e18 ÷ 1e6)
= 135000e18 x 1e18 ÷ (50000 x 1e18)
= 135000e18 ÷ 50000
= 2.7e18If the current ratio (2.7) is less than the target ratio (3), then rChange is 1. rChange is used to determine whether it needs to add or remove liquidity from one side of tranche.
rChange = (currentRatio(t, rate, sFactorA, sFactorB) < t.targetRatio) ? 1 : 0;deltaA is equal to abs(tranche.reserveA, (tranche.reserveB ÷ rate x tranche.targetRatio)) ÷ (1 + tranche.targetRatio)
deltaA = (
Math.abs(t.reserveA, tokenAForTokenB(t.reserveB, t.targetRatio, rate, sFactorA, sFactorB)) * sFactorA
) / (sFactorA + (t.targetRatio * sFactorA / sFactorI));function tokenAForTokenB(
uint256 amountB,
uint256 ratio,
uint256 rate,
uint256 sFactorA,
uint256 sFactorB
) internal pure returns(uint256) {
return (((amountB * sFactorI / sFactorB) * ratio) / rate) * sFactorA / sFactorI;
}deltaB is equal to deltaA x rate.
deltaB = ((deltaA * sFactorB / sFactorA) * rate) / sFactorI;Filling in all the known numbers, we have
// Given USDC, which ETH is required such that USDC / ETH is equal to the ratio
tokenAForTokenB = (((50000e6 x 1e18 ÷ 1e6) x 3e18) ÷ 1800e18) x 1e18 ÷ 1e18
= 50000e18 x 3e18 ÷ 1800e18
= 150000e36 ÷ 1800e18
= 83.333333333e18
deltaA = Math.abs(75e18, 83.333333333e18) x 1e18 ÷ (1e18 + (3e18 x 1e18 ÷ 1e18))
= 8.3333333e18 x 1e18 ÷ 4e18
= 2.0833333e18
deltaB = ((2.0833333e18 x 1e6 ÷ 1e18) x 1800e18) ÷ 1e18
= 2.0833333e6 x 1800
= 3749.99994e6That means it needs to add 2.0833333 ETH and remove 3749.99994 USDC to meet the target ratio. To prove that the ratio is correct, let’s try to calculate the ratio with the new reserves.
new ETH = 75 + 2.0833333 = 77.0833333
new ETH value in USDC = 77.0833333 x 1800 = 138749.99994
new USDC = 50000 - 3749.99994 = 46250.00006
new ratio = 138749.99994 ÷ 46250.00006 = 2.99999999481 (≈3)Since totalDeltaA is > 0 and totalDeltaB is < 0, the final result is
(deltaA, deltaB, rChange) = (uint256(totalDeltaA), uint256(-totalDeltaB), 1);and the rate of change is
rDiv = (totalReserveA == 0) ? 0 : deltaA * EPoolLibrary.sFactorI / totalReserveA;
= 2.0833333e18 x 1e18 ÷ 75e18
= 0.02777777733e18
= 2.78%Now that we know how many USDC it needs to swap for USDC, it can go ahead and perform the flash swap.
IUniswapV2Pair pair = IUniswapV2Pair(factory.getPair(address(tokenA), address(tokenB)));
uint256 amountOut0; uint256 amountOut1;
(amountOut0, amountOut1) = (address(tokenA) == pair.token0())
? (deltaA, uint256(0)) : (uint256(0), deltaA);
bytes memory data = abi.encode(ePool, fracDelta);
pair.swap(amountOut0, amountOut1, address(this), data);By providing data bytes as the last argument, Sushiswap knows it is a flash swap and it will send a callback to EPoolPeriphery (uniswapV2Call function) with the same data bytes.
The callback function has to first verify the call is for an approved tranche by decoding the data and checking the ePool address.
(IEPool ePool, uint256 fracDelta) = abi.decode(data, (IEPool, uint256));
require(ePools[address(ePool)], "EPoolPeriphery: unapproved EPool");Then it calls EPool#rebalance to rebalance the tranche. For a rebalance to be successful, the rate of change has to be greater than the minimum rate of change threshold and the current rebalance has to be at least rebalanceInterval seconds away from the last rebalance. The function accepts an argument fracDelta in case the rebalancer does not want to perform 100% of the rebalance, but we will assume it to be a full rebalance in this article.
We will not go into details on the math of rebalancing tranches as it is the same as the delta calculation previously. Just note that it loops through all the tranches, calculates their corresponding deltaA and deltaB, and then updates their reserves.
for (uint256 i = 0; i < tranchesByIndex.length; i++) {
Tranche storage t = tranches[tranchesByIndex[i]];
totalReserveA += t.reserveA;
(uint256 _deltaA, uint256 _deltaB, uint256 _rChange) = _trancheDelta(t, fracDelta);
if (_rChange == 0) {
(t.reserveA, t.reserveB) = (t.reserveA - _deltaA, t.reserveB + _deltaB);
(totalDeltaA, totalDeltaB) = (totalDeltaA - int256(_deltaA), totalDeltaB + int256(_deltaB));
} else {
(t.reserveA, t.reserveB) = (t.reserveA + _deltaA, t.reserveB - _deltaB);
(totalDeltaA, totalDeltaB) = (totalDeltaA + int256(_deltaA), totalDeltaB - int256(_deltaB));
}
}After calculating the necessary info, the function does its rate of change and timestamp check.
(deltaA, deltaB, rChange, rDiv) = _rebalanceTranches(fracDelta);
require(rDiv >= rebalanceMinRDiv, "EPool: minRDiv not met");
require(block.timestamp >= lastRebalance + rebalanceInterval, "EPool: within interval");Because it is adding ETH and removing USDC, the function transfers ETH from the periphery to the pool and sends USDC from the pool to the periphery.
tokenA.safeTransferFrom(msg.sender, address(this), deltaA);
tokenB.safeTransfer(msg.sender, deltaB);Back to the callback function, it has to determine the amount of USDC to repay Sushiswap. It does so by calling Sushiswap router’s getAmountsIn function.
address[] memory path = new address[](2); // [0] flash swap repay token, [1] flash lent token
uint256 amountsIn; // flash swap repay amount
uint256 deltaOut;
// add ETH, release USDC to EPool -> flash swap ETH, repay with USDC
path[0] = address(ePool.tokenB()); path[1] = address(ePool.tokenA());
(amountsIn, deltaOut) = (router.getAmountsIn(deltaA, path)[0], deltaB);deltaOut is the amount of USDC transferred out from the pool, if the amount to repay Sushiswap is greater than deltaOut, it needs to get a subsidy from the Keeper subsidy pool. Otherwise it will transfer the surplus to the Keeper subsidy pool for any deficits in the future. The function checks the slippage between the repay amount and the actual amount transferred out from the pool is not greater than its max flash swap slippage threshold.
if (amountsIn > deltaOut) {
require(
amountsIn * EPoolLibrary.sFactorI / deltaOut <= maxFlashSwapSlippage,
"EPoolPeriphery: excessive slippage"
);
keeperSubsidyPool.requestSubsidy(path[0], amountsIn - deltaOut);
} else if (amountsIn < deltaOut) {
IERC20(path[0]).safeTransfer(address(keeperSubsidyPool), deltaOut - amountsIn);
}Finally, it repays the flash swap. Failing to repay will revert the whole transaction.
IERC20(path[0]).safeTransfer(msg.sender, amountsIn);Closing Thoughts
BarnBridge’s SMART Exposure allows users to easily rebalance their portfolios. Rebalancing is automatically taken care for regularly, without users having to do complex calculations and going through multiple transactions to swap just to lose money on slippage. Changing your exposure is also as easy as swapping your exposure token for another exposure token with a different target ratio. They are just ERC-20 tokens in the end. The ability to turn risk exposure into a token simplifies the lives of many investors who rely on a fixed asset ratio as their investment strategy.